scludam.synthetic module

Module for synthetic data generation.

Contains some helpful functions and distributions and the main classes for generating synthetic sky region samples with an star field and star clusters.

scludam.synthetic.is_inside_circle(center: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]], radius: Number, data: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[bool]][source]

Check if data is inside a circle.

Parameters:

center (Vector2) – list, touple of numpy array of 2 number elements, representing the center of the circle
radius (Number) – radius of the circle
data (Union[Vector2, Vector2Array]) – numpy numeric array of shape (n, 2) to check if inside the circle

Returns:

mask indicating if data is inside the circle.

Return type:

NDArray[bool]

scludam.synthetic.is_inside_sphere(center: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]], radius: Number, data: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[bool]][source]

Check if data is inside a sphere.

Parameters:

center (Vector3) – list, touple of numpy array of 3 number elements, representing the center of the sphere
radius (Number) – radius of the sphere
data (Union[Vector3, Vector3Array]) – numeric array of shape (n, 3) to check if inside the sphere

Returns:

mask indicating if data is inside the sphere.

Return type:

NDArray[bool]

scludam.synthetic.cartesian_to_polar(coords: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Convert cartesian coordinates to polar coordinates.

Cartesian coordinates are taken as (x, y, z) in parsecs in ICRS system and are transformed to (ra, dec, parallax).

Parameters:: coords (Union[Vector3, Vector3Array]) – cartesian coordinates in (x, y, z) in parsecs in ICRS system to be transformed to (ra, dec, parallax).
Returns:: polar coordinates in (ra, dec, parallax).
Return type:: Union[Vector3, Vector3Array]

scludam.synthetic.polar_to_cartesian(coords: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Convert polar coordinates to cartesian coordinates.

Polar coordinates are taken as (ra, dec, parallax) in (degree, degree, mas) in ICRS system and are transformed to (x, y, z) in parsecs in ICRS system.

Parameters:: coords (Union[Vector3, Vector3Array]) – polar coordinates in (ra, dec, parallax) in (degree, degree, mas) in ICRS system.
Returns:: cartesian coordinates in (x, y, z) in parsecs in ICRS system.
Return type:: Union[Vector3, Vector3Array]

class scludam.synthetic.EDSD(w0: float, wl: float, wf: float, **kwargs)[source]

Bases: rv_continuous

Class to represent the EDSD distribution.

Variables:

w0 (float) – Distribution zero point that indicates the lower limit
wl (float) – Parameter that determines the width and the peak at wl/4 of the profile
wf (float) – Distribution final point that indicates the upper limit

Returns:

Distribution object

Return type:

EDSD

Raises:

ValueError – If wf < w0, or if a and b, which determine de evaluation domain in scipy.rv_continuous, do not verify a < w0, b > wf and b > a.

Notes

Exponentially Decreasing Space Density is used to represent certain distributions, such as a parallax distribution of a star catalogue [1] [2]. The EDSD distribution is defined as:

f(w) = wl**3 / 2*(w-w0)**4 * exp(-wl/(w-w0)) if w > w0 and w < wf
f(w) = 0 if w <= w0
f(w) = 0 if w >= wf

where:

w: parallax in mas
w0: distribution zero point that indicates the lower limit
wl: parameter that determines the width and the peak at wl/4 of the profile
wf: distribution final point that indicates the upper limit from which the distribution is zero. This is added to make the function domain limited to [w0, wf], so other values outside this range are not evaluated.

References

Examples

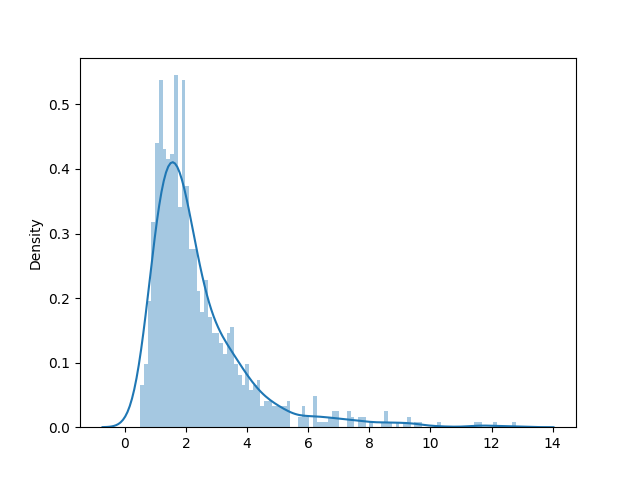
import matplotlib.pyplot as plt
import seaborn as sns

from scludam.synthetic import EDSD

edsd = EDSD(w0=0, wl=5, wf=14)
data = edsd.rvs(1000)
sns.distplot(data, bins=100)
plt.show()

pdf(x: Number | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the EDSD distribution.

Parameters:: x (Union[Number, Numeric1DArray]) – Data to be evaluated.
Returns:: PDF values.
Return type:: Numeric1DArray

Notes

The PDF is defined as the density profile given in [1] [2], but it is not used for random generation. Instead, a Percent Point Function approximation is used.

cdf(x: Number | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Cumulative distribution function.

Parameters:: x (Numeric1DArray)
Returns:: Cumulative distribution function.
Return type:: Numeric1DArray

Notes

The CDF is a polinomial approximation of the real CDF function.

ppf(y: Number | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Percent point function.

Parameters:: y (Numeric1DArray)
Returns:: Percent point function.
Return type:: Numeric1DArray

Notes

The PPF is a polinomial approximation of the real PPF. As cdf and ppf are approximations, one is close to the inverse of the other, but not exactly.

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random variates from the EDSD distribution.

Parameters:: size (int, optional) – Size of the sample, by default 1
Returns:: Generated sample.
Return type:: Numeric1DArray

class scludam.synthetic.UniformSphere(center: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (0.0, 0.0, 0.0), radius: Number = 1.0)[source]

Bases: multi_rv_frozen

Class to represent the Uniform Sphere distribution.

Variables:

center (Vector3) – Center of the sphere.
radius (Number) – Radius of the sphere.

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random sample from the Uniform Sphere distribution.

Parameters:: size (int, optional) – Number of samples to be generated, by default 1
Returns:: Numpy numeric array of shape (size, 3) with the samples.
Return type:: Vector3Array

pdf(x: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Uniform Sphere distribution.

Is calculated as 0 if the point is outside the sphere, and 1 divided by the volume of the sphere otherwise.

Parameters:: x (Union[Vector3, Vector3Array]) – Data to be evaluated
Returns:: Numpy numeric array of shape (size,) with the pdf values.
Return type:: Numeric1DArray

class scludam.synthetic.UniformFrustum(locs: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]], scales: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]], max_size_per_iter: int = 10000000)[source]

Bases: multi_rv_frozen

Class to represent the Uniform Frustum distribution.

It was defined to represent a square sky region sample. It represents a uniform distribution inside a pyramidal frustum.

Variables:

locs (Vector3) – Reference corner of the frustum. It is given by (ra, dec, parallax) polar coordinates in ICRS system, in (degree, degree, mas).
scales (Vector3) – Size of the frustum in (ra, dec, parallax) polar coordinates in ICRS, in (degree, degree, mas).
max_size_per_iter (int, optional) – Maximum number of samples to be generated per iteration, by default 1e7. A bigger value can reduce the amount of time needed to generate the sample, but take more memory.

Examples

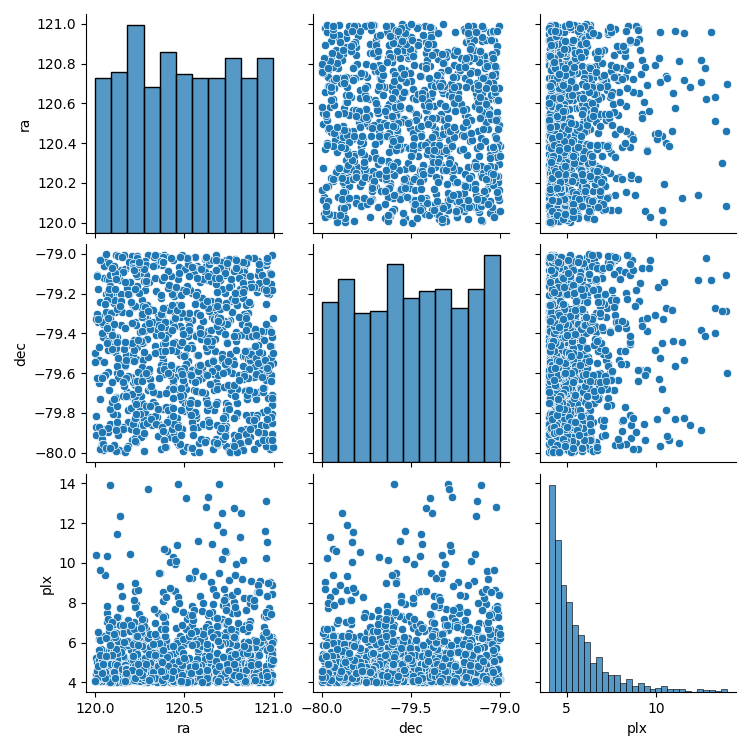
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

from scludam.synthetic import UniformFrustum, cartesian_to_polar

# parallax between 14 and 4 arcsec
uf = UniformFrustum(locs=(120, -80, 14), scales=(1, 1, -10))
# points in cartesian coordinates in parsecs
data = uf.rvs(1000)
# distribution in spherical coordinates
sns.pairplot(pd.DataFrame(cartesian_to_polar(data), columns=["ra", "dec", "plx"]))
plt.show()

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random sample from the Uniform Frustum distribution.

Parameters:: size (int, optional) – size of the random sample, by default 1
Returns:: numpy numeric array of shape (size, 3) with the samples.
Return type:: Vector3Array
Raises:: ValueError – If the given locs are not a valid ICRS coordinate.

pdf(data: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Uniform Frustum distribution.

It is defined as 1 / volume of the frustum for the points inside the frustum, and 0 for the points outside.

Parameters:: data (Union[Vector3, Vector3Array]) – numpy numeric array to be evaluated.
Returns:: PFD values.
Return type:: Numeric1DArray
Raises:: ValueError – If the given locs are not a valid ICRS coordinate.

class scludam.synthetic.UniformCircle(center: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (0.0, 0.0), radius: Number = 1.0)[source]

Bases: multi_rv_frozen

Uniform Circle distribution.

Variables:

center (Vector2) – center of the circle.
radius (Number) – radius of the circle.

pdf(x: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Uniform Circle distribution.

It is defined as 1 / (pi * radius^2) for the points inside the circle, and 0 for the points outside.

Parameters:: x (Union[Vector2, Vector2Array]) – numpy numeric array to be evaluated.
Returns:: Numpy numeric array of shape with the pdf values.
Return type:: Numeric1DArray

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random sample from the Uniform Circle distribution.

Parameters:: size (int, optional) – size of the random sample, by default 1
Returns:: Numpy numeric array of shape (size, 2) with the samples.
Return type:: Vector2Array

class scludam.synthetic.BivariateUniform(locs: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (0.0, 0.0), scales: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (1.0, 1.0))[source]

Bases: multi_rv_frozen

Bivariate Uniform distribution.

Variables:

locs (Vector2) – center of the bivariate uniform distribution.
scales (Vector2) – scale of the bivariate uniform distribution.

Returns:

instance of the Bivariate Uniform distribution.

Return type:

BivariateUniform

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random sample from the Bivariate Uniform distribution.

Parameters:: size (int, optional) – size of the sample, by default 1
Returns:: numpy array of shape (size, 2) with the samples.
Return type:: Vector2Array

pdf(x: Tuple[Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Bivariate Uniform distribution.

Parameters:: x (Union[Vector2, Vector2Array]) – data to be evaluated.
Returns:: numpy array with the pdf values.
Return type:: Numeric1DArray

class scludam.synthetic.TrivariateUniform(locs: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (0.0, 0.0, 0.0), scales: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] = (1.0, 1.0, 1.0))[source]

Bases: multi_rv_frozen

Trivariate Uniform distribution.

Variables:

locs (Vector3) – center of the trivariate uniform distribution.
scales (Vector3) – scale of the trivariate uniform distribution.

Returns:

instance of the Trivariate Uniform distribution.

Return type:

TrivariateUniform

rvs(size: int = 1) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Generate random sample from the Trivariate Uniform distribution.

Parameters:: size (int, optional) – size of the sample, by default 1
Returns:: Numpy array of shape (size, 3) with the samples.
Return type:: Vector3Array

pdf(x: Tuple[Number, Number, Number] | List[numbers.Number][List[Number]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]] | ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]]) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Trivariate Uniform distribution.

Is defined as 1 / volume for the points inside the volume, and 0 for the points outside.

Parameters:: x (Union[Vector3, Vector3Array]) – Points to be evaluated.
Returns:: Numpy array with the pdf values.
Return type:: Numeric1DArray

class scludam.synthetic.StarCluster(space: multi_rv_frozen, pm: multi_rv_frozen, representation_type: str = 'spherical', n_stars: int = 200)[source]

Bases: object

Class for generating astrometric data from a star cluster.

Variables:

space (stats._multivariate.multi_rv_frozen) – Space distribution of the cluster. It must have 3 dimensions.
pm (stats._multivariate.multi_rv_frozen) – Proper motion distribution of the cluster. It must have 3 dimensions.
representation_type (str) – Type of representation of the cluster. It must be “spherical” or “cartesian”, by default “spherical”.

Returns:

An instance of the StarCluster class.

Return type:

StarCluster

rvs() → DataFrame[source]

Generate random sample from the Star Cluster distribution.

Returns:: Data frame with the samples.
Return type:: pd.DataFrame

pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Joint probability density function of the StarCluster distribution.

Parameters:: data (pd.DataFrame) – Data to be evaluated. Must contain the columns “ra”, “dec”, “parallax” or “x”, “y”, “z”, and “pmra”, “pmdec”.
Returns:: PDF values for the data.
Return type:: Numeric1DArray

pm_pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Proper Motion distribution.

Parameters:: data (pd.DataFrame) – Data to be evaluated.
Returns:: PDF values for the data.
Return type:: Numeric1DArray

space_pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the space distribution.

Parameters:: data (pd.DataFrame) – Data to be evaluated. Must have columns “x”, “y”, “z” or “ra”, “dec”, “parallax”.
Returns:: PDF values for the data.
Return type:: Numeric1DArray

class scludam.synthetic.StarField(space: multi_rv_frozen, pm: multi_rv_frozen, representation_type: str = 'spherical', n_stars: int = 100000)[source]

Bases: object

Class for generating star field data.

Variables:

space (stats._multivariate.multi_rv_frozen) – Distribution of the space coordinates. Must have 3 dimensions.
pm (stats._multivariate.multi_rv_frozen) – Distribution of the proper motion coordinates. Must have 2 dimensions.
representation_type (str) – Type of representation of the spatial data. Must be “cartesian” or “spherical”, by default “spherical”.

Returns:

An instance of the StarField class.

Return type:

StarField

rvs() → DataFrame[source]

Generate random sample from the Star Field distribution.

Returns:: Contains columns for the space distrubution and the pm distribution.
Return type:: pd.DataFrame

pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Joint Probability Density Function of the Star Field.

Parameters:: data (pd.DataFrame) – Data to be evaluated.
Returns:: PDF values for the data.
Return type:: Numeric1DArray

pm_pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the Proper Motion distribution.

Parameters:: data (pd.DataFrame) – Data to be evaluated. Must have columns “pmra” and “pmdec”.
Returns:: PDF of the Proper Motion distribution.
Return type:: Numeric1DArray

space_pdf(data: DataFrame) → ndarray[Any, dtype[number]][ndarray[Any, dtype[number]]][source]

Probability density function of the space distribution.

Parameters:: data (pd.DataFrame) – Data to be evaluated. Must have columns “x”, “y”, “z” or “ra”, “dec”, “parallax”.
Returns:: PDF of the space distribution.
Return type:: Numeric1DArray

class scludam.synthetic.Synthetic(star_field: StarField, representation_type: str = 'spherical', clusters: List[StarCluster] = _Nothing.NOTHING)[source]

Bases: object

Class for generating synthetic data.

Variables:

space (stats._multivariate.multi_rv_frozen) – The space distribution, it must be a 3d distribution.
pm (stats._multivariate.multi_rv_frozen) – The proper motion distribution, it must be a 2d distribution.
representation_type (str) – The representation type, it must be “cartesian” or “spherical”, by default is “spherical”.

Examples

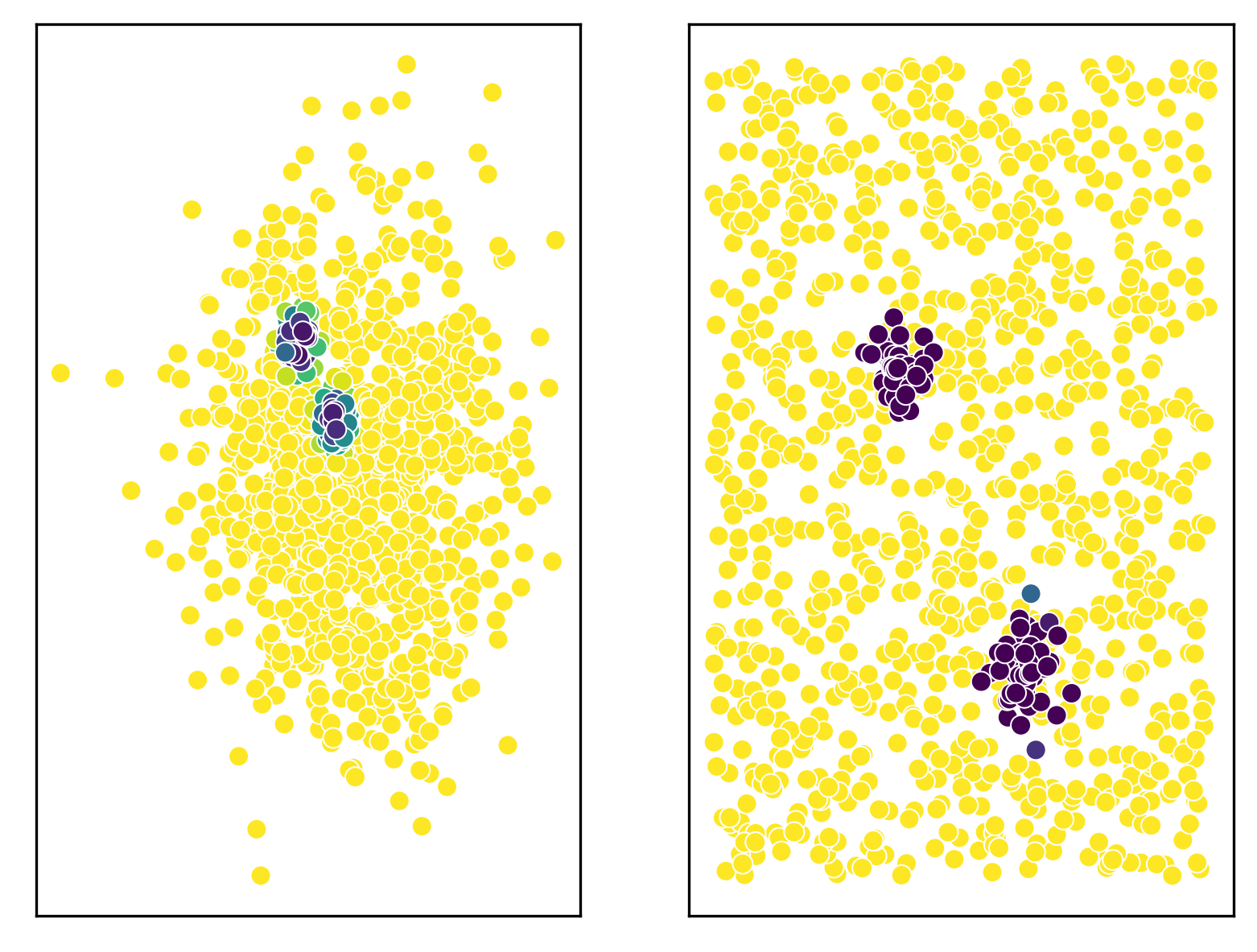
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import multivariate_normal

from scludam.synthetic import (
    StarCluster,
    StarField,
    Synthetic,
    UniformFrustum,
    polar_to_cartesian,
)

data = Synthetic(
    star_field=StarField(
        pm=multivariate_normal((-5, 6), cov=3.0),
        space=UniformFrustum(locs=(118, -31, 8), scales=(2, 2, -7)),
        n_stars=1000,
    ),
    clusters=[
        StarCluster(
            space=multivariate_normal(
                mean=polar_to_cartesian([118.75, -29.75, 1.5]), cov=1 / 3
            ),
            pm=multivariate_normal(mean=(-5.4, 6.75), cov=1.0 / 34),
            n_stars=50,
        ),
        StarCluster(
            space=multivariate_normal(
                mean=polar_to_cartesian([119.25, -30.5, 2]), cov=1 / 3
            ),
            pm=multivariate_normal(mean=(-6.25, 7.75), cov=1.0 / 34),
            n_stars=50,
        ),
    ],
    representation_type="spherical",
).rvs()

fig, ax = plt.subplots(ncols=2)
sns.scatterplot(
    data=data, x="pmra", y="pmdec", hue="p_pm_field", palette="viridis", ax=ax[0]
)
sns.scatterplot(
    data=data, x="ra", y="dec", hue="p_space_field", palette="viridis", ax=ax[1]
)
plt.show()

rvs() → DataFrame[source]

Generate synthetic data from field and cluster distributions.

Returns:: synthetic data with columns for the space distribution, the proper motion distribution and approximations of the membership probabilities without taking into account any errors.
Return type:: pd.DataFrame